オイラーの公式
ブログ紹介
初めまして、Hyper-Positive-Yancyです。大学時代数学から目を背けていたツケがたたり、今更必死こいて勉強する羽目になっております。
このブログでは、備忘録程度に、高校数学〜大学教養レベルの数学の知識かつ数検に役立ちそうなものを書き留めていきます。何か目に留まるものがあったら是非感想や意見を!修正が必要な箇所は遠慮なくその旨をお伝えください。
さて、記念すべき第一回は、オイラーの公式です。単に定理の紹介だけでは尺が微妙なので、よくあるやつですが、三角関数の加法定理の導出まで紹介しようと思います。
オイラーの公式

オイラーの公式は、上記のように指数関数と三角関数を結びつける式で、複素解析において非常に重要な役割を担っていおります。これは複素数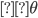 について一般になりたちますが、特に
について一般になりたちますが、特に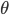 が実数の時には複素平面上の偏角となります。複素平面に関しては今後また別の記事で詳しく扱う予定です。
が実数の時には複素平面上の偏角となります。複素平面に関しては今後また別の記事で詳しく扱う予定です。
オイラーの公式で、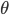 を
を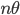 に置き換えると、
に置き換えると、
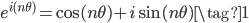
が得られます。これは後に用いる重要な性質です。
さて、オイラーの公式で  とおくと、以下のオイラーの等式(ちょっとややこしい笑)が導かれます。
とおくと、以下のオイラーの等式(ちょっとややこしい笑)が導かれます。
オイラーの等式
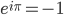
この式は小川洋子氏の小説、もしくはその映画版である『博士の愛した数式』にも登場しますし、数学に馴染みのない方でも知っているよという人は多い印象です。オイラーの公式よりも、その特殊なケースであるこの式の方が、よく話題に上るのはなぜでしょうか? それはおそらく、左辺と右辺の質の違いでしょう。左辺は二つの無理数であるネイピア数( )、円周率(
)、円周率(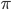 )と、虚数単位
)と、虚数単位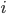 によって表現されています。にも関わらず右辺は、
によって表現されています。にも関わらず右辺は、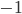 というシンプル極まりない実数です!直感からは想像すらつかないこの帰結に畏敬の念すら覚えます。
というシンプル極まりない実数です!直感からは想像すらつかないこの帰結に畏敬の念すら覚えます。
三角関数とオイラーの公式
さて、次にオイラーの公式と三角関数を結び付けたいと思います。先ほどの(1)式 で 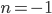 とすると、
とすると、
\begin{eqnarray}e^{-i\theta} &=& \cos \theta + i \sin \theta \\&=&\cos (-\theta) + i \sin (-\theta)\\&=&\cos \theta - i\sin \theta\end{eqnarray}\tag{2}
オイラーの公式自体と(2)の和をとると、
\begin{array}{cc} \ & e^{i\theta} = \cos \theta + i \sin \theta \\+) \ & e^{-i\theta} = \cos \theta - i \sin \theta \\\hline \ & e^{i\theta} + e^{-i\theta} = 2\cos \theta\end{array}
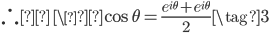
同様に、差をとると、
\begin{array}{cc} \ & e^{i\theta} = \cos \theta + i \sin \theta \\-) \ & e^{-i\theta} = \cos \theta - i \sin \theta \\\hline\ & e^{i\theta} - e^{-i\theta} = 2i \sin \theta\end{array}
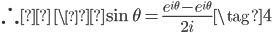
となり、三角関数は指数関数によって表現できる。
加法定理の導入
オイラーの公式で  と置き換えると、
と置き換えると、

上記の左辺を、(1)を用いて書き下すと、
\begin{eqnarray}
e^{i(\alpha + \beta)}&=&e^{i\alpha}e^{i\beta}\\ &=&(\cos \alpha + i \sin \alpha)(\cos \beta + i \sin \beta) \\
&=&(\cos \alpha \cos \beta - \sin \alpha \sin \beta ) - i(\sin \alpha \cos \beta + \cos \alpha\sin \beta)
\end{eqnarray} \tag{a}
(a) の実部と虚部を比較すると、加法定理が得られる。
\begin{eqnarray}\cos(\alpha + \beta) &= \cos \alpha \cos\beta - \sin \alpha \sin \beta \\\sin(\alpha + \beta) &=\sin \alpha \cos \beta + \cos \alpha \sin \beta \end{eqnarray}
おわりに
このブログでは、以上のように、数学の基本的なことをまとめていこうと思います。また、入試や数検の問題の解説的なこともしたいなと思っております。解いてほしい問題や扱ってほしい題材も募集しております!!それではまた〜⭐️